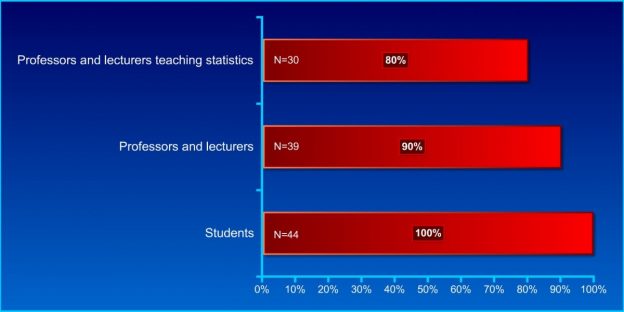
NHST: Irrational orthodoxy vs. Bayesian statistics

The majority of professors who lecture statistics are unable to interpret a simple t-test correctly as the following empirical data illustrates (adapted from Haller & Krauss, 2002).

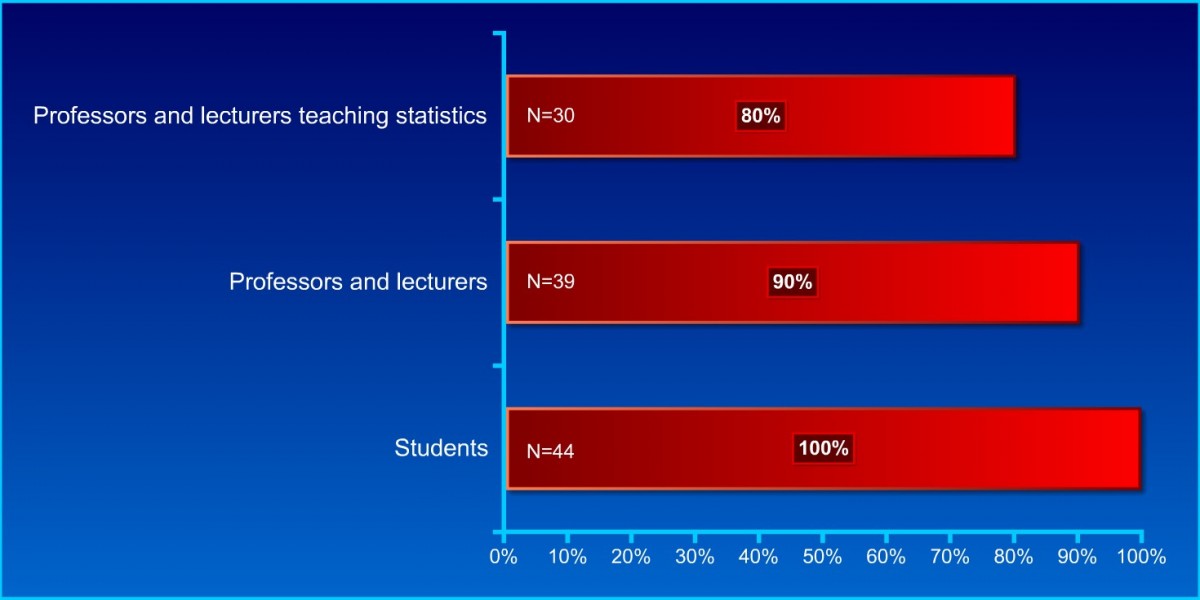Figure 1. Fallacious statistical reasoning in the interpretation of an independent samples t-test (Haller & Krauss, 2002).

“Teaching statistics to psychology students should not only consist of teaching
calculations, procedures and formulas, but should focus much more on statistical
thinking and understanding of the methods…Since thinking as well as understanding are genuine matters of scientific psychology, it is astounding that these issues have been largely neglected in the methodology instruction of psychology students.” (Haller & Krauss, 2002, p.17)

Haller, H., & Krauss, S. (2002). Misinterpretations of significance: a problem students share with their teachers? Methods of Psychological Research Online, 7(1), 1–20.
https://www.metheval.uni-jena.de/lehre/0405-ws/evaluationuebung/haller.pdf

Recommended publications

Bakan, D. (1966). The test of significance in psychological research. Psychological
Bulletin, 66, 423-437.
Cohen, J. (1994). The Earth Is Round (p < .05). American Psychologist, 49(12), 997–1003. https://doi.org/10.1037/0003-066X.49.12.997
Gigerenzer, G. (1998). We need statistical thinking, not statistical rituals. Behavioral and Brain Sciences, 21(2), 199–200. https://doi.org/10.1017/S0140525X98281167

What Null Hypothesis Significance Testing Does Not Tell Us

It does not give us the probability that our results are due to chance.
If we reject H₀ with α = 0.05 this does not mean that we are 95 % sure that the alternative hypothesis is true.
Rejecting H₀ with α = 0.05 does not mean that the probability that we have made a type I error is 5 %.
A p-value does not tell us that our findings are relevant, clinical significant or of any scientific value whatsoever.
A small p-value does not tell us our results will replicate.
A small p-value does not indicate a large treatment effect.
Failing to reject the null hypothesis is not evidence of it being true.
If our test has 80 % power and we fail to reject the null hypothesis, then this does not mean that the probability is 20 % that the null is true.
If our test has 80 % power and we do reject the null hypothesis, then this does not mean that the probability is 80 % that the alternative hypothesis is true.

Some prominent NHST testimonials

“What’s wrong with [null hypothesis significance testing]? Well, among many other things, it does not tell us what we want to know, and we so much want to know what we want to know that, out of desperation, we nevertheless believe that it does!”
– Cohen (1994)

“… surely the most bone-headedly misguided procedure ever institutionalized in the rote training of science students”
– Rozeboom (1997)

“… despite the awesome pre-eminence this method has attained in our journals and textbooks of applied statistics, it is based upon a fundamental misunderstanding of the nature of rational inference, and is seldom if ever appropriate to the aims of scientific research”
– Rozeboom (1960)

“… an instance of a kind of essential mindlessness in the conduct of research”
– Bakan (1966)

“Statistical significance testing retards the growth of scientific knowledge; it never makes a positive contribution”
– Schmidt and Hunter (1997)

“The textbooks are wrong. The teaching is wrong. The seminar you just attended is wrong. The most prestigious journal in your scientific field is wrong.”
– Ziliak and McCloskey (2008)

For more information on the topic see:

Gigerenzer, G., Krauss, S., & Vitouch, O. (2004). The null ritual: What you always wanted to know about null hypothesis testing but were afraid to ask. In D. Kaplan (ed.), Handbook on quantitative methods in the social sciences (pp. 391–408). Thousand Oaks, CA: Sage.
Oakes, M. (1986). Statistical inference: A commentary for the social and behavioral sciences. New York: Wiley.

Abstract word cloud for P-value with related tags and terms

What is wrong with NHST?

It does not tell us what we want to know, and we so much want to know what we want to know that, out of desperation, we nevertheless believe that it does! What we want to know is “Given these data, what is the probability that H0 is true?”
However, what it tells us is “Given that H0 is true, what is the probability of these (or more extreme) data?“ These are not the same as has been pointed out many times over the years by Meehl (1978, 1986, 1990a, 1990b), Gigerenzer (1993), and Cohen (1990).

Why 5%?

How did Fisher come up with the 5% p-value. Well, it all boils down to a cup of English tea.