See also my project http://belief-bias.de
Every man prefers belief to the exercise of judgment.
We speak not strictly and philosophically when we talk of the combat of passion and of reason. Reason is, and ought only to be the slave of the passions, and can never pretend to any other office than to serve and obey them.
A well studied phenomenon in the psychology of reasoning is termed belief bias (Evans et al., 1983; Markovits & Nantel, 1989). Belief bias labels the long standing effect that reasoners are more likely to accept a believable conclusion to a syllogism than an unbelievable one, independent of the actual logical validity of the conclusion (i.e. Wilkins, 1928; Henle & Michael, 1956; Kaufman & Goldstein, 1967). For instance, examination of the following syllogism (see appendix for some basic definitions) shows that this argument is logically invalid and that its conclusion does not concord with belief. Consequently, endorsement rates are very low for this type of problem.
Major premise: No police dogs are vicious.
Minor premise: Some highly trained dogs are vicious.
________________________________________________________
Conclusion: ∴ Some police dogs are not highly trained.
Interestingly, one can construct syllogisms in which validity and believability are discordant, as in the following argument:
Major premise: No addictive things are inexpensive.
Minor premise: Some cigarettes are inexpensive.
_________________________________________________________
Conclusion: ∴ Some addictive things are not cigarettes.
In this example the syllogism is logically invalid (i.e., a non sequitur) but the conclusion is believable. Upon inspection, it can be determined that the two exemplary syllogisms have the same logical form. Despite this fact, a major proportion of participants judge the fallacious but believable conclusion as valid, i.e., participants exhibit the tendency to judge the validity of a syllogism based on its a priori believability. In their classic research on belief bias Evans et al. (1983) reported two main effects, first, participants affirm more believable than unbelievable conclusions and, second, more logically valid than invalid conclusions. Moreover, there was a significant interaction between believability and validity. The effects of belief are stronger on logically invalid than on valid syllogisms. This phenomenon is one of the most prevalent content effects studied in deductive reasoning (for a comprehensive review see Klauer et al., 2000) and it has been demonstrated that response bias to a given syllogism can be influenced by several factors, for example, perceived difficulty of the syllogism (Evans, 2009a), caution (Pollard & Evans, 1980), atmosphere bias (Begg & Denny, 1969), figural bias (Dickstein, 1978; Morley et al., 2004; Jia et al., 2009), presentation order (Lambell et al., 1999), and perceived base rate of valid syllogisms (Klauer et al., 2000), to name just the most prominent factors.
A widely acknowledged descriptive explanation for the belief bias effect is termed the default interventionist (DI) account (see Evans, 2007). Following this account Type 1 and Type 2 processes succeed one another in a sequential order. Primacy is attributed to Type 1 (heuristic) processes which generate a default response whereas recency is ascribed to Type 2 (analytic) processes which approve or override the response generated by Type 1 processes (Stanovich & West, 2000; De Neys, 2006; Evans, 2007; Stanovich, 2008). The process of computing the correct solution and overriding the response cued by Type 1 processes is assumed to be costly in cognitive terms, drawing on limited executive resources. The DI process model is visualized in Figure 1.

Figure 1. Flowchart depicting the default-interventionist model.
Appendix
The goal of Aristotle’s main works (and of all logic) is to formalize validity. Validity does not guarantee truth but truth preservation. If the premise is true then the conclusion has to be true. What makes an argument valid is structure and not content. Syntax vs. semantics. In other words, the core idea of logic is that validity is a matter of form. Therefore, one can make a completely valid argument consisting of nonsense terms.
Standard form syllogism
Hypothetical modus ponens
A modus ponens (from the Latin ponere, meaning “to affirm”) rule of inference has the following form:
If P, then Q. (1st premise)
P. (2nd premise)
Ergo, Q. (conclusion)
It can be formally written in sequent notation (Sanford, 2003):
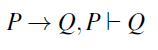
That means whenever you accept P you are forced to accept Q. For example, If apples cost £20 a kilo then your name is Peter. Suppose apples cost £20 a kilo. Your name would be Peter then, wouldn’t it? (example adapted from Bornat, 2005, p. 30) The validity of arguments in the modus ponens form can be illustrated in a truth table.

Truth table
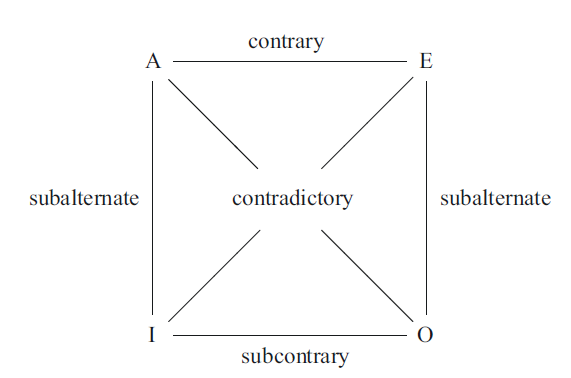
A categorical syllogism consists of three categorical propositions. Two of these propositions constitute the premises, or the basis of the inference that can be drawn. The other proposition is offered as the conclusion (the result). These propositions are traditionally labeled A, E I, and O. The A and the I are both affirmative and A and I are the first two vowels in the Latin term affirmo (I affirm). The E and O propositions, on the other hand, are both negative and they are the vowels in the Latin term nego (I deny) (Copi & Cohen, 1994).
A valid argument is put together in such a way that the truth of its premises forces the truth of its conclusion. In other words, if the premises are true the conclusion has to be true (validity occurs with closure). For instance, when the premises in the syllogism depicted in Table 6b are true there is no way to avoid that the conclusion is true as well. Note that the word “Greeks” (the middle term) bridges the gap between the minor term (Athenians) and the major term (mortals). In other words, the minor term and major term are linked by a connector which is labeled the middle term and it occurs in both premises. The middle term is like an intermediate link in a chain through which the connection between minor term and major term is made.

Logic of syllogisms
Looking for the rational foundations of knowledge Aristotle observed that the validity of a syllogism depends on a limited number of rules. If any of these rules is violated a syllogism is invalid. However, if each of these rules is met then the syllogism flies (is valid). Aristotle mapped out in detail these rules which differentiate between standard form syllogisms which are valid and those that are not. One of these rules applies to distribution. Distribution refers to whether or not a categorical statement claims something about each and every member of a class that it refers to. If a categorical statement does that it is said to be distributive if it does not it is said to be undistributive. For instance, an A proposition distributes its subject term but not its predicate term. The distribution patterns capture the relationship of contradictoriness. In other word, the distribution patterns in two contradictory statements are exactly reversed.