
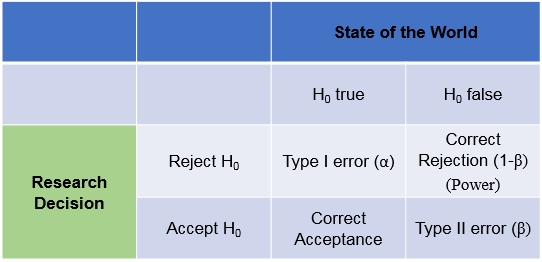
Definition of Type I error:
Probability of rejecting null hypothesis when it is TRUE.
Definition of Type II error:
Probability of not rejecting null hypothesis when it is False.
Imagine tests on 1000 hypotheses 100 of which are true.
The tests have a false positive rate of 5%. That means they produce 45 false positives (5% of 900). They have a power of .8, so they can confirm only 80 of the true hypotheses, producing 20 negatives.
Not knowing what is false and what is not the researcher sees 125 hypotheses as true, 45 of which are not. The negative results are much more reliable but less likely to be published.

A parable concerning editorial policies
There’s this desert prison, see, with an old prisoner, resigned to his life, and a young one just arrived. The young one talks constantly of escape, and, after a few months, he makes a break. He’s gone a week, and then he’s brought back by the guards. He’s half dead, crazy with hunger and thirst. He describes how awful it was to the old prisoner. The endless stretches of sand, no oasis, no signs of life anywhere. The old prisoner listens for a while, then says, Yep, I know. I tried to escape myself, twenty years ago. The young prisoner says, You did? Why didn’t you tell me, all these months I was planning my escape? Why didn’t you let me know it was impossible? And the old prisoner shrugs, and says, So who publishes negative results? (Hudson, 1968, p. 168)
Hudson, J. A. (1968). A Case of Need. New York: The New American Library Inc.

Simulation in R
Download R: https://www.r-project.org/
Type I error
n=1000 # testing 1000 times
t1err=0
for (i in 1:n){
x=rnorm(100, 0, 1)
if (((t.test(x, mu=0))$p.value)<=0.05) (t1err=t1err+1)
}
cat("Type I error rate in percentage is", (t1err/n)*100,"%")
Type II error
n=1000 # testing 1000 times
t2err=0
for (i in 1:n){
x=rnorm(100, 2, 1)
if (((t.test(x, mu=0))$p.value)>0.05) (t2err=t2err+1)
}
cat("Type II error rate in percentage is", (t2err/n)*100,"%")
