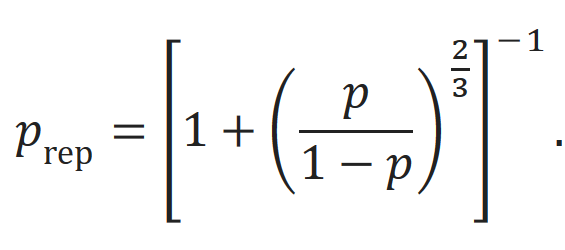The primary objective of p_rep is to provide an estimate of replicability (based on the empirical data) which does not involve Bayesian assumptions with regards to a priori distributions of θ. The submission guidelines of the APA flagship journal ‘Psychological Science’ for some time explicitly encouraged authors to “use prep rather than p-values” in the results section of their articles. This factoid is documented in the internet archive, a digital library which provides a mnemonic online system containing the history of the web, a “digital time machine” (Rackley, 2009; Rogers, 2017). However, this official statistical recommendation by Psychological Science has now been retracted (but the internet never forgets…).

The URL of the relevant internet archive entry is as follows:
https://web.archive.org/web/20060525043648/http://www.blackwellpublishing.com/submit.asp?ref=0956-7976

By default, the prep metric is based upon a one-tailed probability value of test statistic T (but it can be used for F-test as well). However, this default can be changed into a two-tailed computation. We used the “psych” package (Revelle, 2015) in R to compute the replication probabilities (two-tailed) according to the following equation (the associated R code can be found below).

However, the mathematical validity of prep has been questioned (Doros & Geier, 2005). Based on the results of simulation studies, it has been convincingly argued that “prep misestimates the probability of replication” and that it “is not a useful statistic for psychological science” (Iverson et al., 2009). In another reply to Killeen’s proposal, it has been suggested that hypothesis testing using Bayes factor analysis is a much more effective strategy to avoid the problems associated with classical p-values (Wagenmakers & Grünwald, 2006). One of the main shortcoming of the suggested new metric is that prep does not contain any new information over and above the p-value, it is merely an extrapolation. Another weakness is that a priori information (for example knowledge from related previous studies) cannot be incorporated. Killeen responds to this argument with the “burden of history” argument, i.e., each result should be investigated in isolation without taking any prior knowledge into account (viz., he advocates uniform priors). However, it is highly questionable whether a single study can be used as a basis for estimating the outcome of future studies. Various confounding factors (e.g., a tertium quid) might have biased the pertinent results and consequently lead to wrong estimates and predictions. Extraordinary claims require extraordinary evidence. The novel prep metric does not align with this Bayesian philosophy. From our point of view, the main advantage to report and discuss prep is that it helps to explicate and counteract the ubiquitous “replication fallacy” (G Gigerenzer, 2004) associated with conventional p-value. The replication fallacy describes the widespread statistical illusion that the p-value contains information about the replicability of experimental results. In my own survey at a CogNovo workshop at the University of Plymouth in 2015 the “replication fallacy” was the most predominant misinterpretations of p-values. 77% (i.e., 14 out of 18) of our participants (including lecturers and professors) committed the replication fallacy. Only one participant interpreted the meaning of p-values correctly, presumably due to random chance. In a rejoinder titled “Replicability, confidence, and priors” (Killeen, 2005b) Killeen addresses several criticisms in some detail, particularly with regards to the stipulated nescience262 of δ. Indeed, it has been argued that “replication probabilities depend on prior probability distributions” and that Killeen’s approach ignores this information and as a result, “seems appropriate only when there is no relevant prior information” (Macdonald, 2005). However, in accordance with the great statisticians of this century (e.g., Cohen, 1994, 1995; Meehl, 1967), we argue that the underlying syllogistic logic of p-values is inherently flawed and that any attempt to rectify p-values is moribund. It is obvious that there is an urgent and long due “need to change current statistical practices in psychology” (Iverson et al., 2009). The current situation is completely intolerable and the ramifications are tremendously wide and complex. New and reflective statistical thinking is needed, instead of repetitive “mindless statistical rituals,” as Gerd Gigerenzer put it (Gigerenzer, 1998, 2004). However, deeply engrained social (statistical) norms are difficult to change, especially when large numbers of researchers have vested interests to protect the prevailing methodological status quo as they were predominantly exclusively trained in the frequentist framework (using SPSS). Hence, a curricular change is an integral part of the solution. Statistical software should by default be flexible enough to perform multiple complementary analyses. SPSS is now capable to interface with R and various Bayesian modules will become available in future versions. This extension of capabilities could have been realised much earlier and one can only speculate why SPSS is non-Bayesian for such a long time. However, given that R is on the rise, SPSS is now forced to change its exnovative approach in order to defend market shares. To conclude this important topic, it should be emphasised that rational approaches vis-à-vis problems associated with replicability, confidence, and the integration of prior knowledge are pivotal for the evolution and incremental progress of science. It is obvious that the fundamental methods of science are currently in upheaval.

function (p = 0.05, n = NULL, twotailed = FALSE)
{
df <- n - 2
if (twotailed)
p <- 2 * p
p.rep <- pnorm(qnorm((1 - p))/sqrt(2))
if (!is.null(n)) {
t <- -qt(p/2, df)
r.equiv <- sqrt(t^2/(t^2 + df))
dprime = 2 * t * sqrt(1/df)
return(list(p.rep = p.rep, d.prime = dprime, r.equiv = r.equiv))
}
else {
return(p.rep)
}
}
<bytecode: 0x0000000015c932f8>
<environment: namespace:psych>

“p.rep” function from the “psych” R package (after Killeen, 2005a)

p.rep
Probability of replication
Dprime (D’)
Effect size (Cohen`s d) if more than just p is specified
prob
Probability of F, t, or r. Note that this can be either the one-tailed or two tailed probability value.
r.equivalent For t-tests, the r equivalent to the t (see Rosenthal and Rubin(2003), Rosnow, Rosenthal, and Rubin, 2000)).
The effect size estimate r.equivalent has been suggested by several authors (Rosenthal & Rubin, 2003; Rosnow, Rosenthal, & Rubin, 2000). It is particularly useful for meta-analytic research. However, it has been criticised on several grounds (Kraemer, 2005). The question of “what should be reported” standardised or simple effect size (Baguley, 2009) is not resolved.
https://www.rdocumentation.org/packages/psych/versions/1.7.8/topics/p.rep