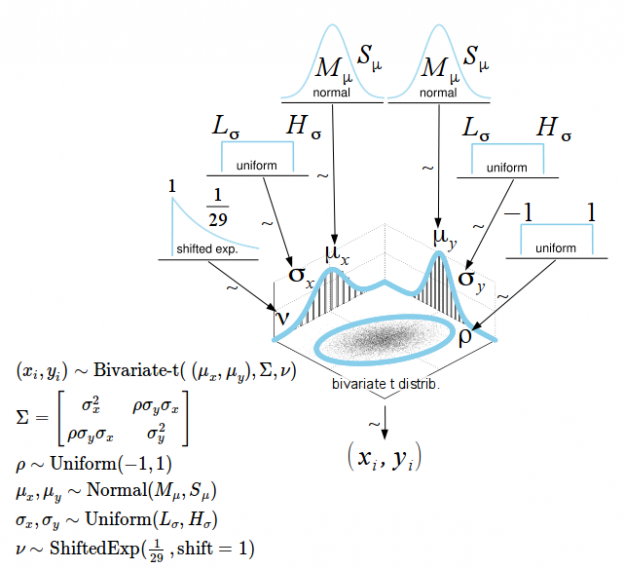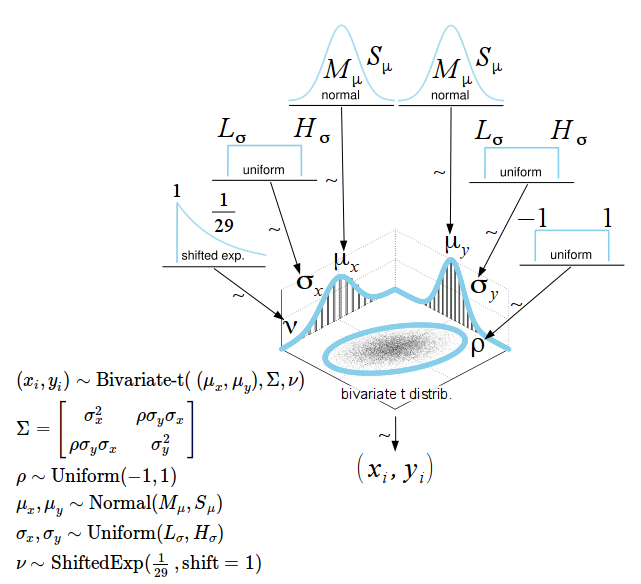
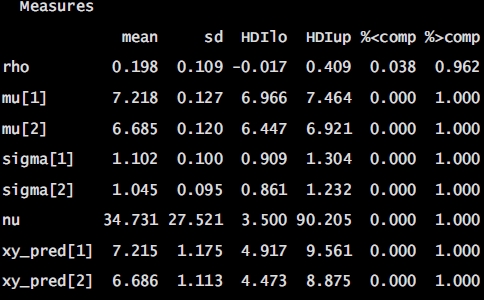
Numerical summary for all parameters associated with experimental condition V01 and V11 and their corresponding 95% posterior high density credible intervals.
• ρ (rho): The correlation between experimental condition V00 and V10
• μ1 (mu[1]): The mean of V00
• σ1 (sigma[1]): The scale of V00, a consistent estimate of SD when nu is large.
• μ2 (mu[2]): the mean of V10
• σ1 (sigma[2]): the scale of V10
• ν (nu): The degrees-of-freedom for the bivariate t distribution
• xy_pred[1]: The posterior predictive distribution of V00
• xy_pred[2]: The posterior predictive distribution of V10
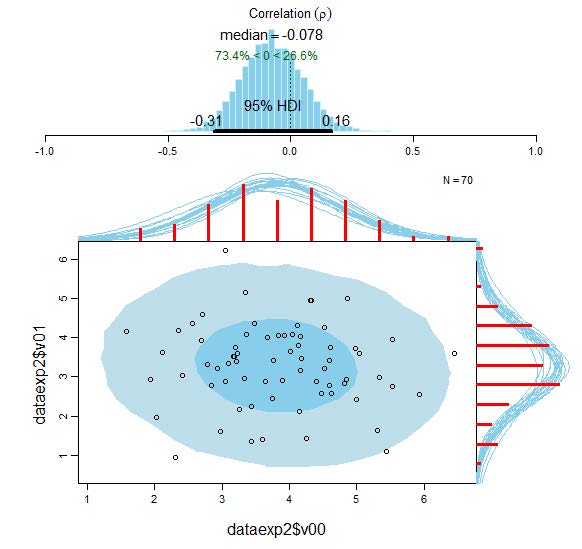
Visualisation of the results of the Bayesian correlational analysis for experimental condition V00 and V01 with associated posterior high density credible intervals and marginal posterior predictive plots.
The upper panel of the plot displays the posterior distribution for the correlation ρ (rho) with its associated 95% HDI. In addition, the lower panel of the plot shows the original empirical data with superimposed posterior predictive distributions. The posteriors predictive distributions allow to predict new data and can also be utilised to assess the model fit. It can be seen that the model fits the data reasonably well. The two histograms (in red) visualise the marginal distributions of the experimental data. The dark-blue ellipse encompasses the 50% highest density region and the light-blue ellipse spans the 95% high density region, thereby providing intuitive visual insights into the probabilistic distribution of the data (Hollowood, 2016). The Bayesian analysis provides much more detailed and precise information compared to the classical frequentist Pearsonian approach.
JAGS model code for the correlational analysis
# Model code for the Bayesian alternative to Pearson's correlation test.
# (Bååth, 2014)
require(rjags)
#(Plummer, 2016)
#download data from webserver and import as table
Dataexp2 <-
read.table("http://www.irrational-decisions.com/phd-thesis/dataexp2.csv", header=TRUE, sep=",", na.strings="NA", dec=".", strip.white=TRUE)
# Setting up the data
x <- dataexp1$v01
y <- dataexp1$v11
xy <- cbind(x, y)
# The model string written in the JAGS language
model_string <- "model {
for(i in 1:n) {
xy[i,1:2] ~ dmt(mu[], prec[ , ], nu)
}
xy_pred[1:2] ~ dmt(mu[], prec[ , ], nu)
# JAGS parameterizes the multivariate t using precision (inverse of variance)
# rather than variance, therefore here inverting the covariance matrix.
prec[1:2,1:2] <- inverse(cov[,])
# Constructing the covariance matrix
cov[1,1] <- sigma[1] * sigma[1]
cov[1,2] <- sigma[1] * sigma[2] * rho
cov[2,1] <- sigma[1] * sigma[2] * rho
cov[2,2] <- sigma[2] * sigma[2]
# Priors
rho ~ dunif(-1, 1)
sigma[1] ~ dunif(sigmaLow, sigmaHigh)
sigma[2] ~ dunif(sigmaLow, sigmaHigh)
mu[1] ~ dnorm(mean_mu, precision_mu)
mu[2] ~ dnorm(mean_mu, precision_mu)
nu <- nuMinusOne+1
nuMinusOne ~ dexp(1/29)
}"
# Initializing the data list and setting parameters for the priors
# that in practice will result in flat priors on mu and sigma.
data_list = list(
xy = xy,
n = length(x),
mean_mu = mean(c(x, y), trim=0.2) ,
precision_mu = 1 / (max(mad(x), mad(y))^2 * 1000000),
sigmaLow = min(mad(x), mad(y)) / 1000 ,
sigmaHigh = max(mad(x), mad(y)) * 1000)
# Initializing parameters to sensible starting values helps the convergence
# of the MCMC sampling. Here using robust estimates of the mean (trimmed)
# and standard deviation (MAD).
inits_list = list(mu=c(mean(x, trim=0.2), mean(y, trim=0.2)), rho=cor(x, y, method="spearman"),
sigma = c(mad(x), mad(y)), nuMinusOne = 5)
# The parameters to monitor.
params <- c("rho", "mu", "sigma", "nu", "xy_pred")
# Running the model
model <- jags.model(textConnection(model_string), data = data_list,
inits = inits_list, n.chains = 3, n.adapt=1000)
update(model, 500)
samples <- coda.samples(model, params, n.iter=5000)
# Inspecting the posterior
plot(samples)
summary(samples)
Pertinent references
Liechty, J. C.. (2004). Bayesian correlation estimation. Biometrika, 91(1), 1–14.
Plain numerical DOI: 10.1093/biomet/91.1.1
DOI URL
directSciHub download
Show/hide publication abstract
“We propose prior probability models for variance-covariance matrices in order to address two important issues. first, the models allow a researcher to represent substantive prior information about the strength of correlations among a set of variables. secondly, even in the absence of such information, the increased flexibility of the models mitigates dependence on strict parametric assumptions in standard prior models. for example, the model allows a posteriori different levels of uncertainty about correlations among different subsets of variables. we achieve this by including a clustering mechanism in the prior probability model. clustering is with respect to variables and pairs of variables. our approach leads to shrinkage towards a mixture structure implied by the clustering. we discuss appropriate posterior simulation schemes to implement posterior inference in the proposed models, including the evaluation of normalising constants that are functions of parameters of interest. the normalising constants result from the restriction that the correlation matrix be positive definite. we discuss examples based on simulated data, a stock return dataset and a population genetics dataset.”
Wetzels, R., & Wagenmakers, E.-J.. (2012). A default Bayesian hypothesis test for correlations and partial correlations. Psychonomic Bulletin & Review, 19(6), 1057–1064.
Plain numerical DOI: 10.3758/s13423-012-0295-x
DOI URL
directSciHub download
Show/hide publication abstract
“We propose a default bayesian hypothesis test for the presence of a correlation or a partial correlation. the test is a direct application of bayesian techniques for variable selection in regression models. the test is easy to apply and yields practical advantages that the standard frequentist tests lack; in particular, the bayesian test can quantify evidence in favor of the null hypothesis and allows researchers to monitor the test results as the data come in. we illustrate the use of the bayesian correlation test with three examples from the psychological literature. computer code and example data are provided in the journal archives.”
Bååth, R.. (2014). Bayesian First Aid : A Package that Implements Bayesian Alternatives to the Classical *. test Functions in R. Proceedings of UseR 2014
Show/hide publication abstract
“This talk will introduce bayesianfirstaid 1 , an r package that implements bayesian alternatives to the most commonly used statistical tests. it is inspired by the best package [2] and is similarly intended both as a practical tool and as a teaching aid. a main feature of the package is that the bayesian alternatives are called in the same way as the corresponding classical test functions, save for the addition of bayes. to the beginning of the function name. for example, if binom.test(x=7, n=10) runs a classical binomial test then bayes.binom.test(x=7, n=10) runs the bayesian alternative. this makes the package easy to pick up and use, especially if you are already used to the classical * .test functions, and it also facilitates comparing the output of the different approaches. all models are implemented using the jags modeling language, called from r using the rjags package. the generic function model.code makes it straightforward to start modifying the models underlying the package. it takes a bayesianfirstaid object and prints out the underlying model code which is ready to be copy-n-pasted into an r script and tinkered with from there. all bayesianfirstaid objects have default plots that show the posteriors of the parameters of interest together with a display that enables a quick posterior predictive check. below is an example of the output from the bayesian first aid alternative to cor.test(…). the data is the hand grip strength (in kg) and index / ring finger ratio for the male group in [1]. > bayes.cor.test(digit_ratio, grip_strength) bayesian first aid pearson correlation coefficient test data: digit_ratio and grip_strength (n = 97) estimated correlation: -0.34 95% credible interval: -0.52 -0.16 the correlation is more than 0 by a probability of 0.001 and less than 0 by a probability of 0.999 > model.code(bayes.cor.test(digit_ratio, grip_strength)) ## bayesian first aid model code ## require(rjags) # setting up the data x <-digit_ratio y <-grip_strength xy <-cbind(x, y) # the model string written in the jags language model_string <-“model { for(i in 1:n) { xy[i,1:2] ~ dmt(mu[], prec[ , ], nu) } > plot(bayes.cor.test(digit_ratio, grip_strength)) [output is truncated] correlation (ρ) −1.0 −0.5 0.0 0.5 1.0 median = −0.344 100% < 0 < 0% 95% hdi −0.518 −0.159 0.85 0.90 0.95 1.00 1.05 20 30 40 50 60 x$x x$y 1 1 digit_ratio probability probability n = 97 grip_strength references [1] hone, l. s. and m. e. mccullough (2012). 2d: 4d ratios predict han…”